Problem Description
We consider an automated warehouse scenario in which robots deliver products to picking stations to fulfill orders. A warehouse is represented as a rectangular grid, and the robots can move between horizontally or vertically adjacent cells. To fulfill given orders, robots have to carry shelves with the required products to matching picking stations. The robots are flat, can move underneath shelves and pick them up. However, a robot that carries a shelf does not fit under another shelf anymore, so that shelves may need to be moved out of the way first. The overall goal is to fulfill all orders in as little time as possible, where time is counted in steps and each robot may (but does not have to) perform one action per time step. While robots move around, pick up and put down shelves, deliver products or remain idle, there must not be collisions, i.e., no robot may move into or switch its cell with another one from one step to the next. Finally, grid cells can be designated as highways, and no shelves may be put down at such cells.
Instance Format
The input consists of facts of the following form, which specify the objects in a warehouse as well as the orders to fulfill:
- init(object(node,'n'),value(at,pair('x','y'))).
- The ground term 'n' labels a grid cell at the coordinates given by positive integers 'x' and 'y'. Taking such facts together, the integers for 'x' and 'y' each start at 1 and specify a rectangular grid without holes.
- init(object(highway,'h'),value(at,pair('x','y'))).
- The ground term 'h' labels a highway cell at the coordinates 'x' and 'y', where a corresponding fact of the first form exists and specifies the grid cell as such.
- init(object(pickingStation,'p'),value(at,pair('x','y'))).
- The ground term 'p' labels a picking station at the cell with coordinates 'x' and 'y', where a corresponding fact of the first form exists and specifies the grid cell as such.
- init(object(robot,'r'),value(at,pair('x','y'))).
- The ground term 'r' labels a robot, initially located at the cell with coordinates 'x' and 'y', where a corresponding fact of the first form exists and specifies the grid cell as such.
- init(object(shelf,'s'),value(at,pair('x','y'))).
- The ground term 's' labels a shelf, initially located at the cell with coordinates 'x' and 'y', where a corresponding fact of the first form exists and specifies the grid cell as such.
- init(object(product,'i'),value(on,pair('s','u'))).
- The ground term 'i' labels a product, of which a positive integer 'u' many units are initially stored on shelf 's', where a corresponding fact of the previous form exists and specifies an initial cell for the shelf. Moreover, the number 'u' of units is unique for each product 'i' and shelf 's', i.e., there is not more than one fact referring to the same product and shelf.
- init(object(order,'o'),value(line,pair('i','u'))).
- The ground term 'o' labels an order, including a positive integer 'u' many units of product 'i', where the number 'u' of units is unique for each order 'o' and product 'i', i.e., there is not more than one fact referring to the same order and product.
- init(object(order,'o'),value(pickingStation,'p')).
- The ground term 'o' labels an order, whose included products ought to be delivered to picking station 'p'. There is exactly one fact of this kind per order 'o' occurring in facts of the previous form, and a fact specifying the cell of picking station 'p' exists as well.
Instances are such that the initial location of a robot or shelf is unique, and no shelf is initially carried by any robot nor located at any cell designated as highway. Moreover, the sum of units of a product 'i' included in orders does not exceed the sum of units of 'i' stored on shelves, so that instances of interest are satisfiable, provided enough time steps (as well as robots and grid space) to carry shelves to picking stations.
Solution Format
A solution consists of the actions of a plan to fulfill all orders. That is, for each product included in an order, robots have to deliver exactly the required number of units, where the delivery can take place in several parts (if multiple units of the same product are included in an order). Actions can be performed at time steps 't' represented by positive integers starting at 1. Each robot (specified by an instance) may, but does not have to, perform one action per time step, and further conditions are described along with the form of atoms for actions in the following:
- occurs(object(robot,'r'),move('dx','dy'),'t').
- At time step 't', the robot labeled 'r' moves from its cell with the coordinates 'x' and 'y', which hosts the robot at time step 't'-1, to the horizontally or vertically adjacent cell with coordinates 'x'+'dx' and 'y'+'dy', where ('dx','dy') ∈ {(1,0),(-1,0),(0,1),(0,-1)}. The coordinates 'x'+'dx' and 'y'+'dy' must refer to a cell belonging to the grid, and no other robot than 'r' must be located at this cell at time step 't'. In case robot 'r' carries a shelf 's', also no other shelf than 's' must be located at the cell with coordinates 'x'+'dx' and 'y'+'dy' at time step 't'. Moreover, for robots 'r1' and 'r2' at cells with the coordinates 'x' and 'y' or 'x'+'dx' and 'y'+'dy', respectively, at time step 't'-1, occurs(object(robot,'r1'),move('dx','dy'),'t') and occurs(object(robot,'r2'),move(-'dx',-'dy'),'t') must not jointly hold, i.e., two robots cannot switch their cells from one step to the next.
- occurs(object(robot,'r'),pickup,'t').
- At time step 't', the robot labeled 'r' picks up the shelf located at its cell with the coordinates 'x' and 'y', which hosts the robot at time step 't'-1. In fact, some shelf must be located at the cell hosting 'r' at time step 't'-1, and robot 'r' must not yet carry this shelf.
- occurs(object(robot,'r'),deliver('o','i','u'),'t').
- At time step 't', the robot labeled 'r' delivers a positive integer 'u' many units of product 'i', included in order 'o'. The cell hosting 'r' at time step 't'-1 must be the cell of the picking station of order 'o'. Moreover, robot 'r' must carry some shelf on which at least 'u' many units of product 'i' are stored at time step 't'-1, and at least 'u' many units of product 'i' must be included in 'o' and yet be undelivered. In fact, the quantity of product 'i' stored on the shelf carried by 'r' and the number of units of 'i' included in order 'o' are both reduced by 'u' at time step 't', and neither of the resulting quantities may be negative.
- occurs(object(robot,'r'),putdown,'t').
- At time step 't', the robot labeled 'r' puts down the shelf it carries at time step 't'-1. Some shelf carried by robot 'r' at time step 't'-1 must exist, and the cell hosting 'r' at time step 't'-1 must not be designated as highway.
The greatest time step 't' occurring within actions of a plan constitutes the makespan of the plan. This makespan is subject to minimization, and a plan is considered better than another if its makespan is smaller. Clearly, a plan needs to be a valid solution in the first place, i.e., all its actions have to executable and all orders must be fulfilled by the plan.
Example
Problem Instance
The below facts specify a 4x4 grid with highways along two of the grid edges. Moreover, cells of the grid host two picking stations, six shelves and two robots. Four different products are stored on the shelves, in particular quantities. The products are subject to three orders: the first consisting of one unit of product 1 and four units of product 3, the second of one unit of product 2, and the third of one unit of product 4. Products in the first order ought to be delivered to the first picking station, and those in the other two orders to the second picking station.
init(object(node,1),value(at,pair(1,1))). init(object(node,2),value(at,pair(2,1))). init(object(node,3),value(at,pair(3,1))). init(object(node,4),value(at,pair(4,1))). init(object(node,5),value(at,pair(1,2))). init(object(node,6),value(at,pair(2,2))). init(object(node,7),value(at,pair(3,2))). init(object(node,8),value(at,pair(4,2))). init(object(node,9),value(at,pair(1,3))). init(object(node,10),value(at,pair(2,3))). init(object(node,11),value(at,pair(3,3))). init(object(node,12),value(at,pair(4,3))). init(object(node,13),value(at,pair(1,4))). init(object(node,14),value(at,pair(2,4))). init(object(node,15),value(at,pair(3,4))). init(object(node,16),value(at,pair(4,4))). init(object(highway,4),value(at,pair(4,1))). init(object(highway,8),value(at,pair(4,2))). init(object(highway,12),value(at,pair(4,3))). init(object(highway,13),value(at,pair(1,4))). init(object(highway,14),value(at,pair(2,4))). init(object(highway,15),value(at,pair(3,4))). init(object(highway,16),value(at,pair(4,4))). init(object(pickingStation,1),value(at,pair(1,3))). init(object(pickingStation,2),value(at,pair(3,1))). init(object(robot,1),value(at,pair(4,3))). init(object(robot,2),value(at,pair(2,2))). init(object(shelf,1),value(at,pair(3,3))). init(object(shelf,2),value(at,pair(2,1))). init(object(shelf,3),value(at,pair(2,3))). init(object(shelf,4),value(at,pair(2,2))). init(object(shelf,5),value(at,pair(3,2))). init(object(shelf,6),value(at,pair(1,2))). init(object(product,1),value(on,pair(3,1))). init(object(product,2),value(on,pair(4,1))). init(object(product,3),value(on,pair(6,4))). init(object(product,4),value(on,pair(5,1))). init(object(product,4),value(on,pair(6,1))). init(object(order,1),value(pickingStation,1)). init(object(order,1),value(line,pair(1,1))). init(object(order,1),value(line,pair(3,4))). init(object(order,2),value(pickingStation,2)). init(object(order,2),value(line,pair(2,1))). init(object(order,3),value(pickingStation,2)). init(object(order,3),value(line,pair(4,1))).
Problem Solution
A plan, which is optimal in terms of makespan, is given by the atoms below, specifying robots' actions at time steps from 1 to 13. In a nutshell, robot 2 first carries shelf 6 to the picking station of the first order and delivers four units of product 3. The first order gets then fulfilled by robot 1, who carries shelf 3 to the same picking station and delivers one unit of product 1. In the sequel, both robots proceed by putting the carried shelves down at different cells and moving towards the second picking station, where products of the other two orders have to be delivered to. The third order gets fulfilled by robot 2, delivering one unit of product 4 from shelf 5. Finally, robot 1 carries shelf 4 to the second picking station and delivers one unit of product 2 to fulfill the second order.
Observe that each of the two robots performs at most one action per time step, where robot 1 remains idle at step 3 and robot 2 at step 13. Moreover, the moves made by the robots are collision-free, i.e., neither do distinct robots or shelves share the same cell at any step nor do robots switch their (adjacent) cells from one step to the next. Also note that the second robot is at a highway cell at step 13, so that putting down shelf 5 would not be admitted.
occurs(object(robot,1),move(-1,0),1). occurs(object(robot,2),move(-1,0),1). occurs(object(robot,1),move(-1,0),2). occurs(object(robot,2),pickup,2). occurs(object(robot,2),move(0,1),3). occurs(object(robot,1),pickup,4). occurs(object(robot,2),deliver(1,3,4),4). occurs(object(robot,1),move(-1,0),5). occurs(object(robot,2),move(0,-1),5). occurs(object(robot,1),deliver(1,1,1),6). occurs(object(robot,2),putdown,6). occurs(object(robot,1),putdown,7). occurs(object(robot,2),move(1,0),7). occurs(object(robot,1),move(1,0),8). occurs(object(robot,2),move(1,0),8). occurs(object(robot,1),move(0,-1),9). occurs(object(robot,2),pickup,9). occurs(object(robot,1),pickup,10). occurs(object(robot,2),move(0,-1),10). occurs(object(robot,1),move(1,0),11). occurs(object(robot,2),deliver(3,4,1),11). occurs(object(robot,1),move(0,-1),12). occurs(object(robot,2),move(1,0),12). occurs(object(robot,1),deliver(2,2,1),13).
Solution Steps
The following images visualize the plan represented by the atoms given above. Steps shown below differ regarding the cells of robots, and actions leading to a particular grid configuration are given on the right of it. The configurations at steps 3/4, 5/6 and 12/13 are shown in one image each, as no moves are made at steps 4, 6 and 13.
| Step 0: | Actions: |
|---|---|
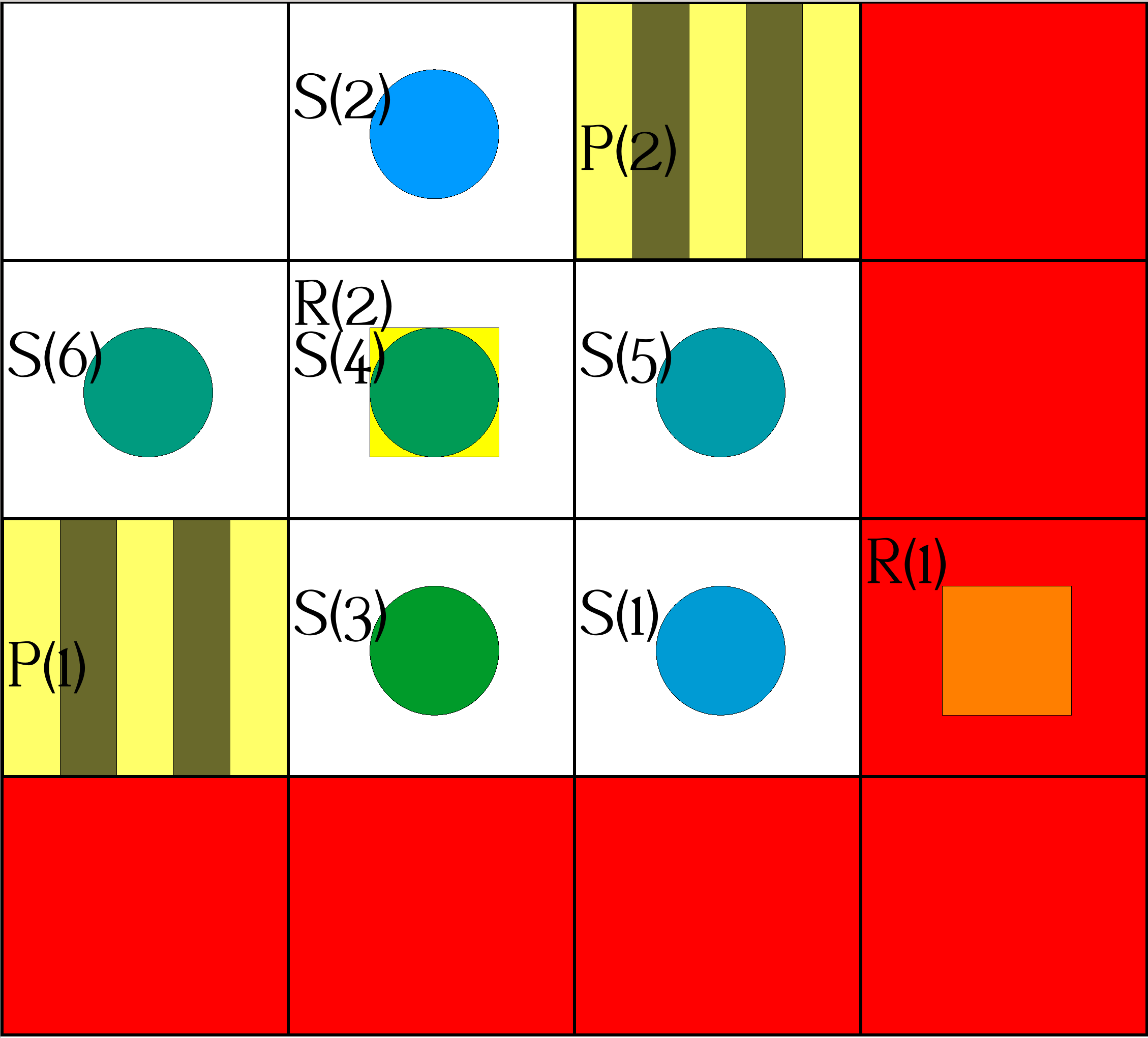 |
|
| Step 1: | Actions: |
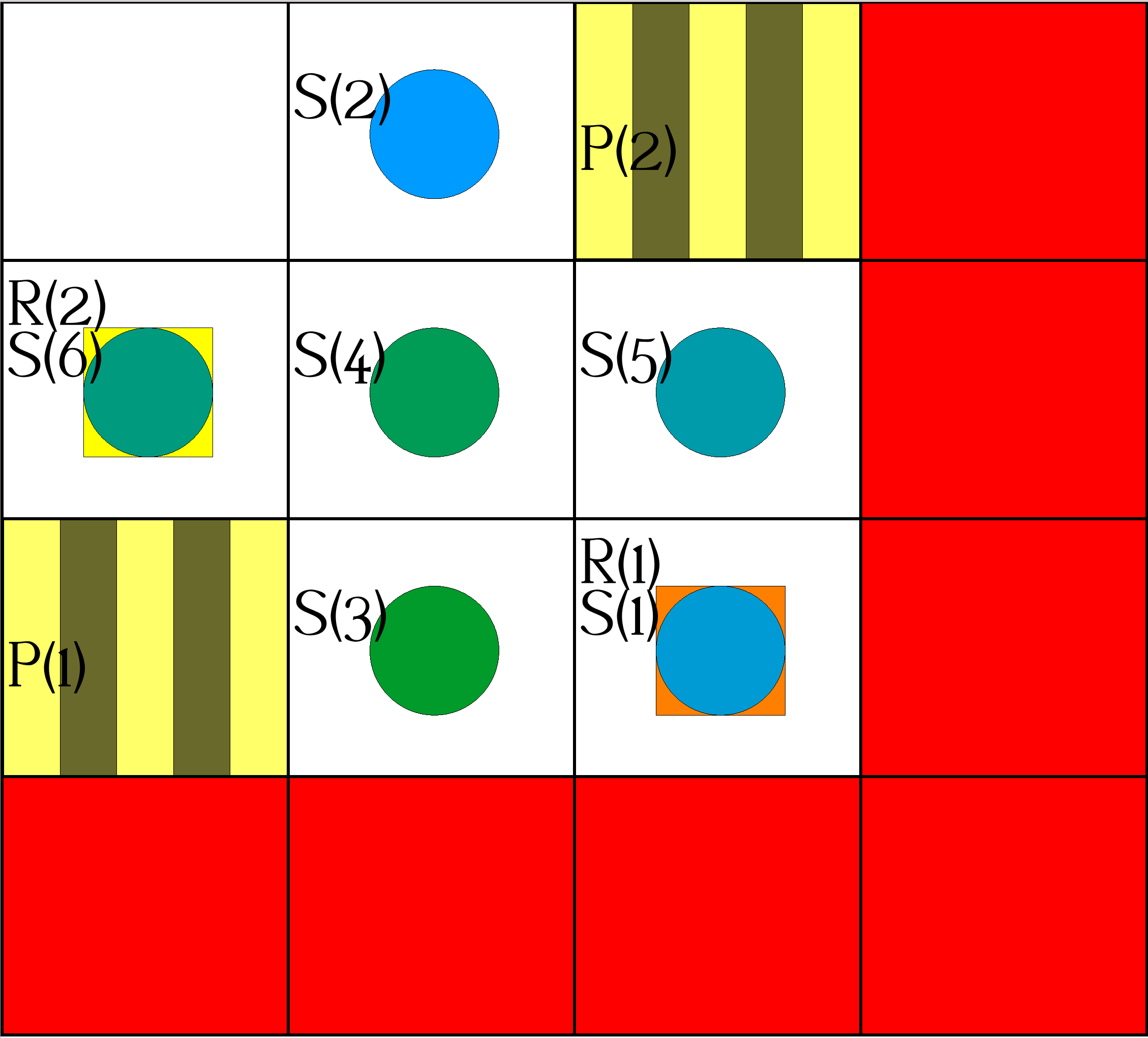 |
occurs(object(robot,1),move(-1,0),1). occurs(object(robot,2),move(-1,0),1). |
| Step 2: | Actions: |
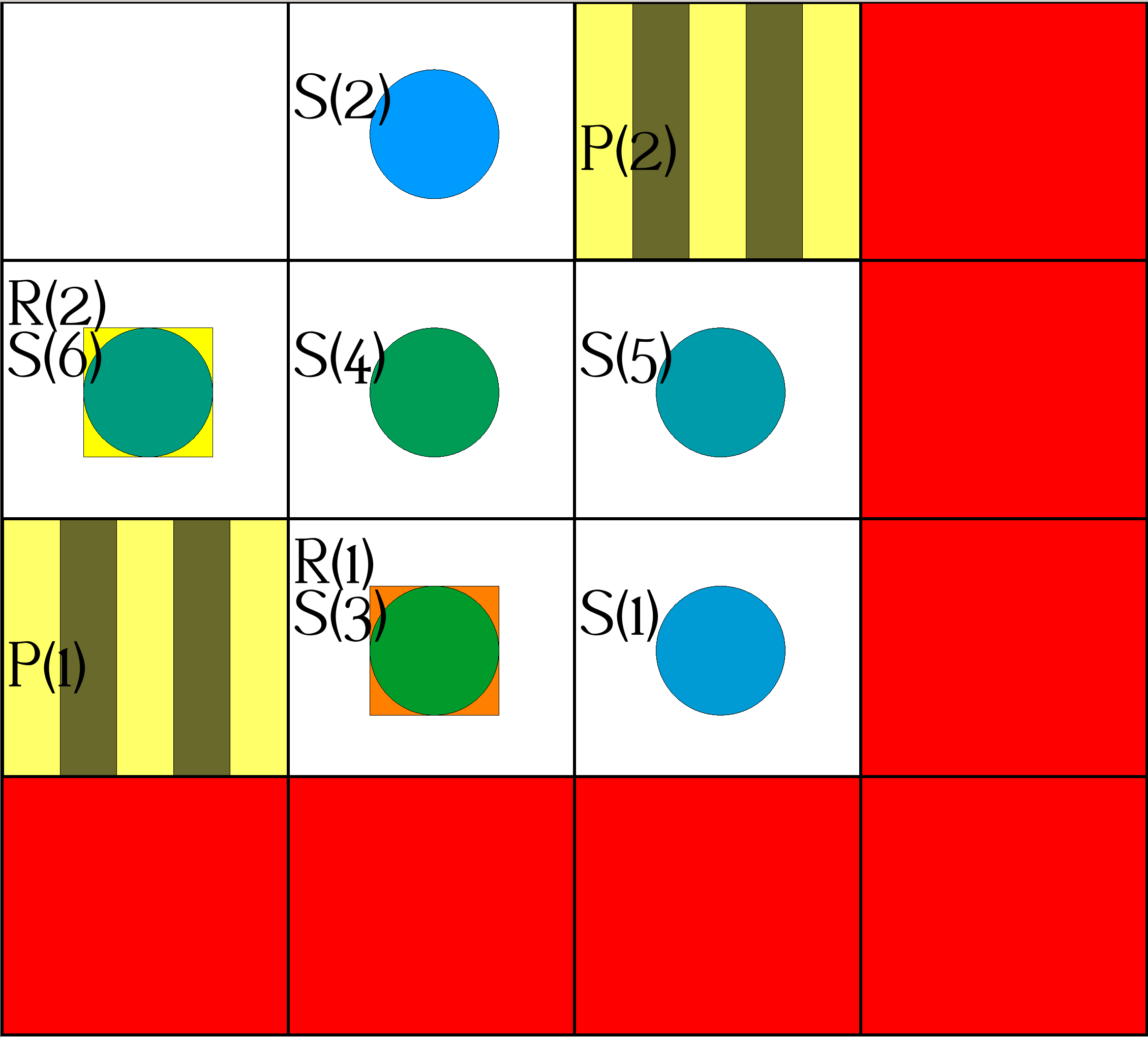 |
occurs(object(robot,1),move(-1,0),2). occurs(object(robot,2),pickup,2). |
| Step 3/4: | Actions: |
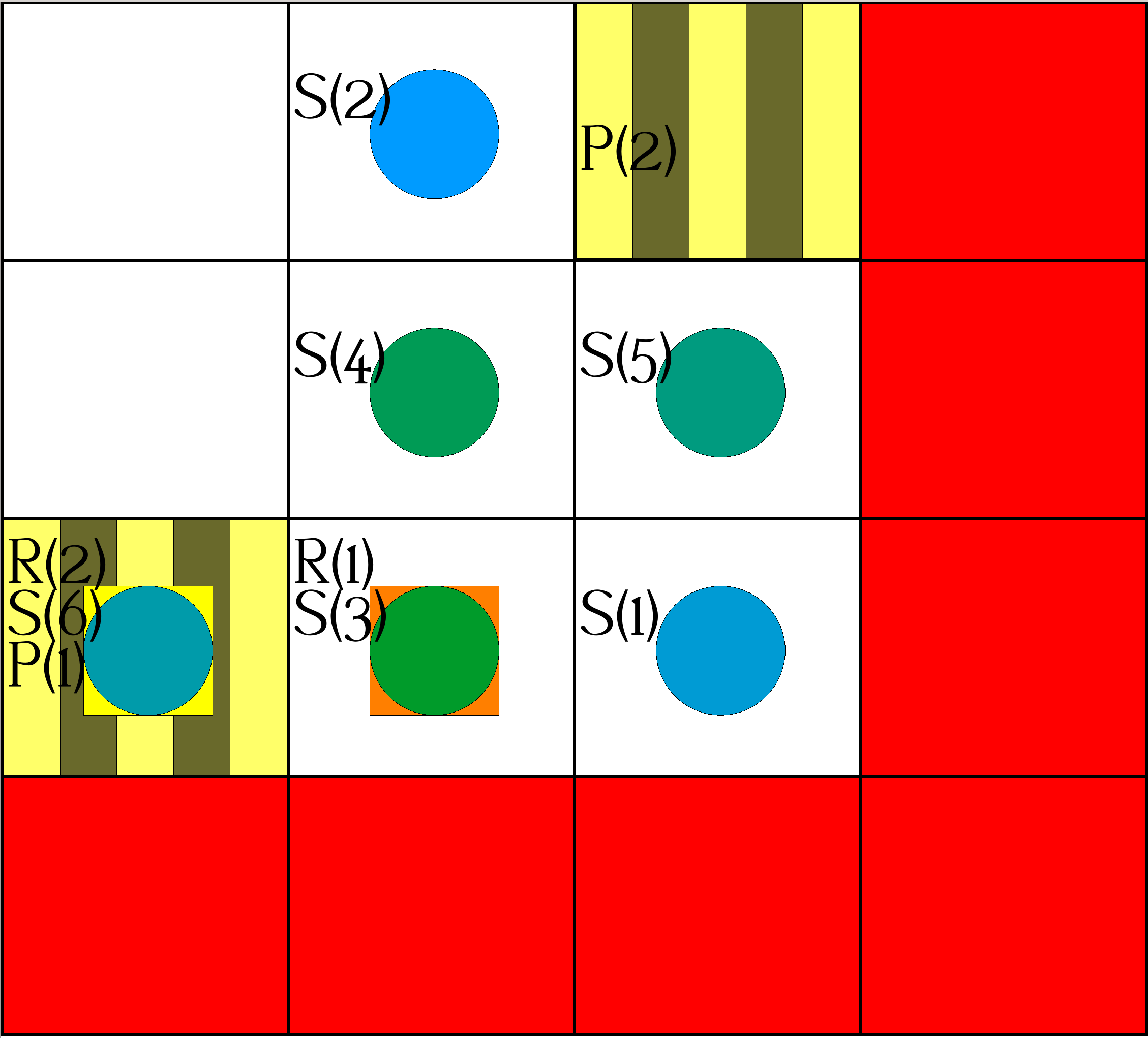 |
occurs(object(robot,2),move(0,1),3). occurs(object(robot,1),pickup,4). occurs(object(robot,2),deliver(1,3,4),4). |
| Step 5/6: | Actions: |
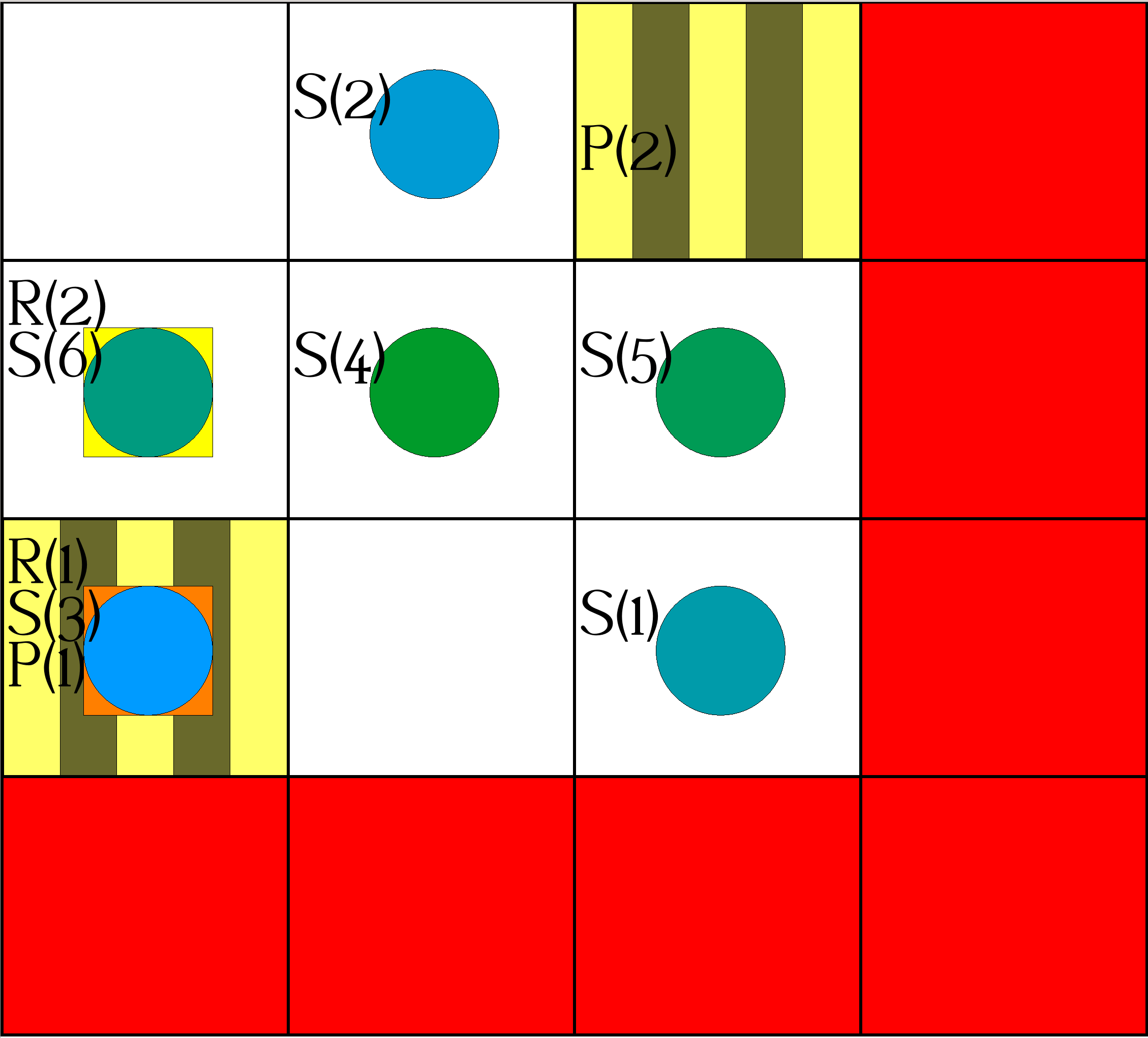 |
occurs(object(robot,1),move(-1,0),5). occurs(object(robot,2),move(0,-1),5). occurs(object(robot,1),deliver(1,1,1),6). occurs(object(robot,2),putdown,6). |
| Step 7: | Actions: |
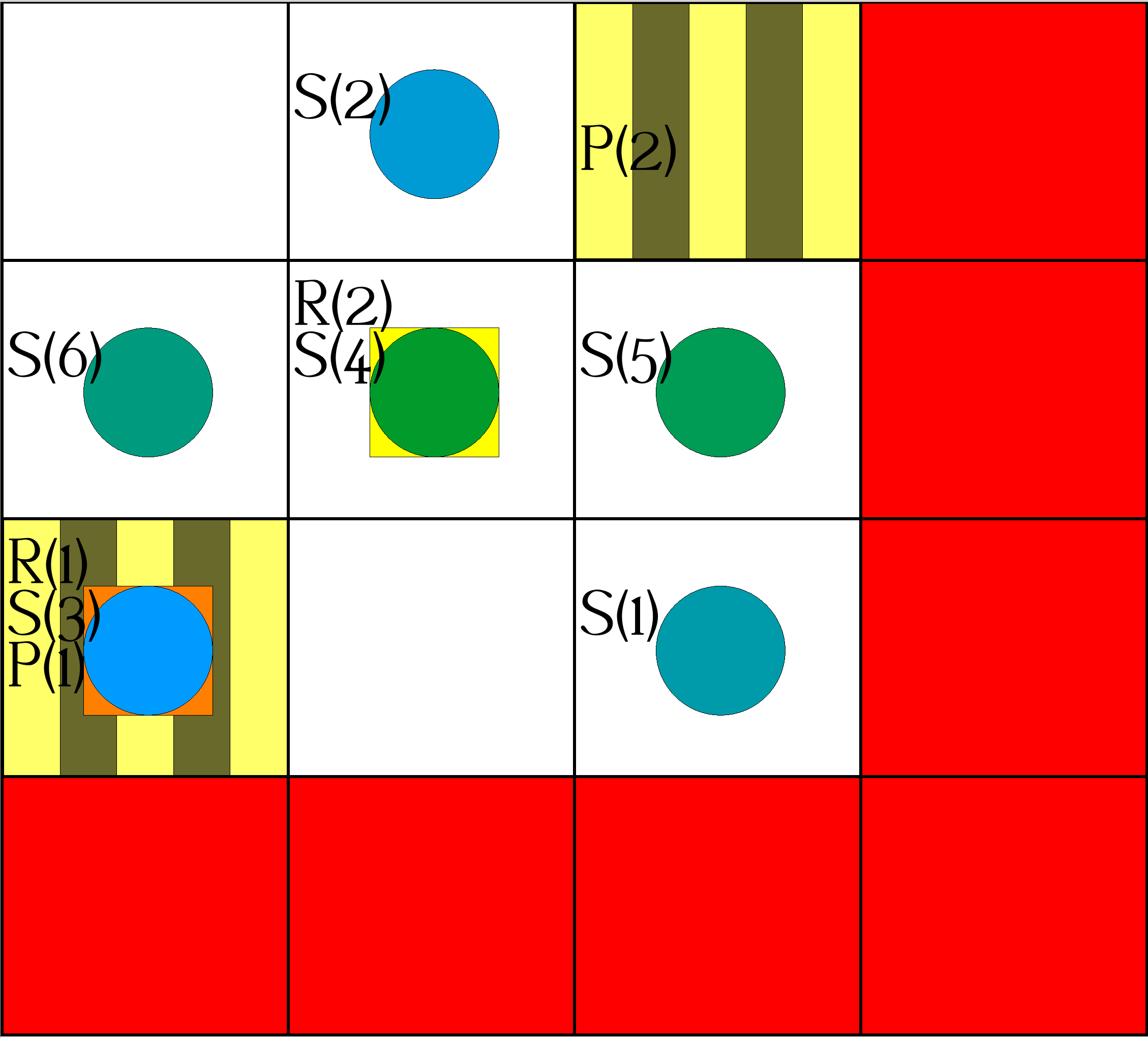 |
occurs(object(robot,1),putdown,7). occurs(object(robot,2),move(1,0),7). |
| Step 8: | Actions: |
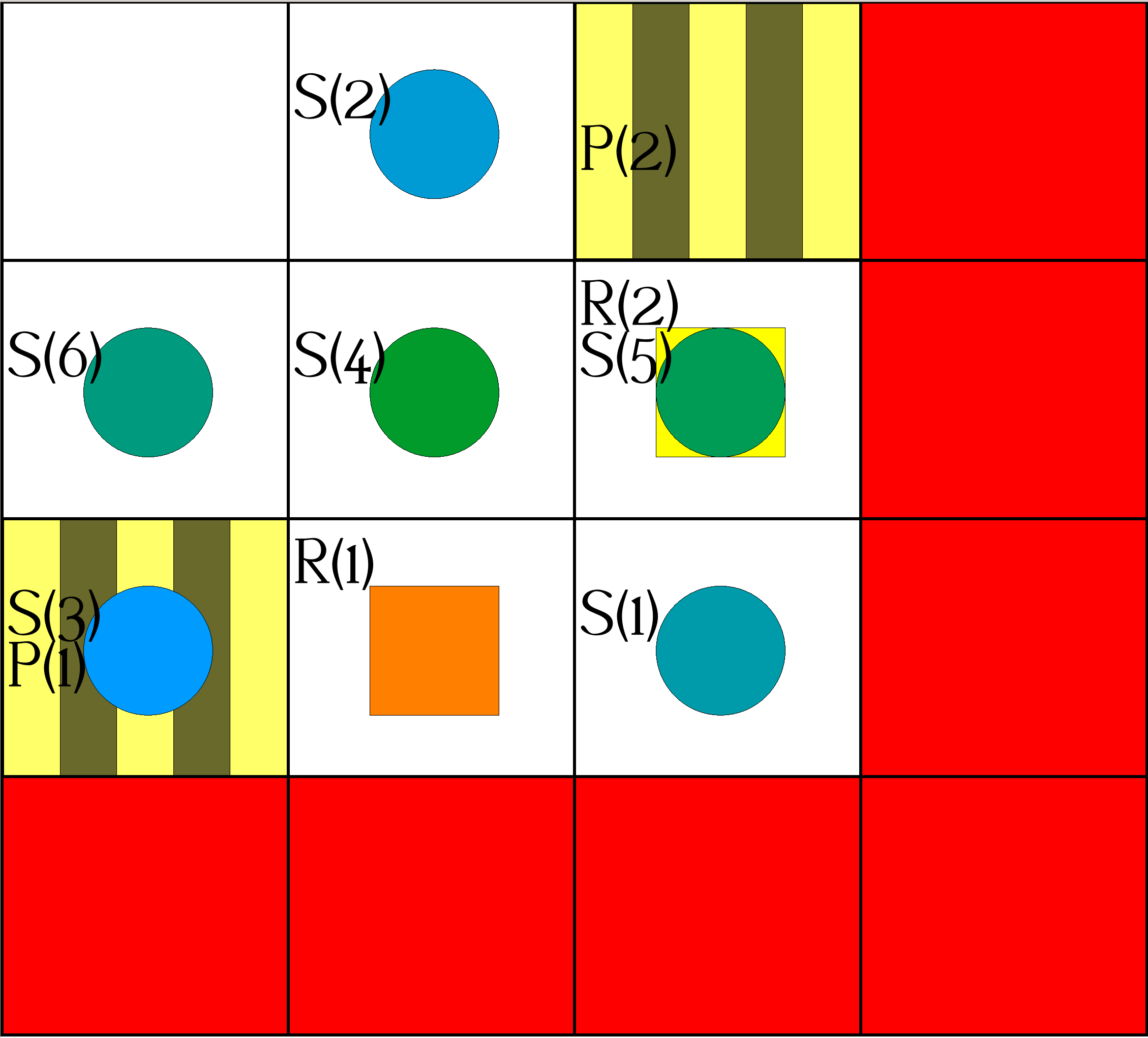 |
occurs(object(robot,1),move(1,0),8). occurs(object(robot,2),move(1,0),8). |
| Step 9: | Actions: |
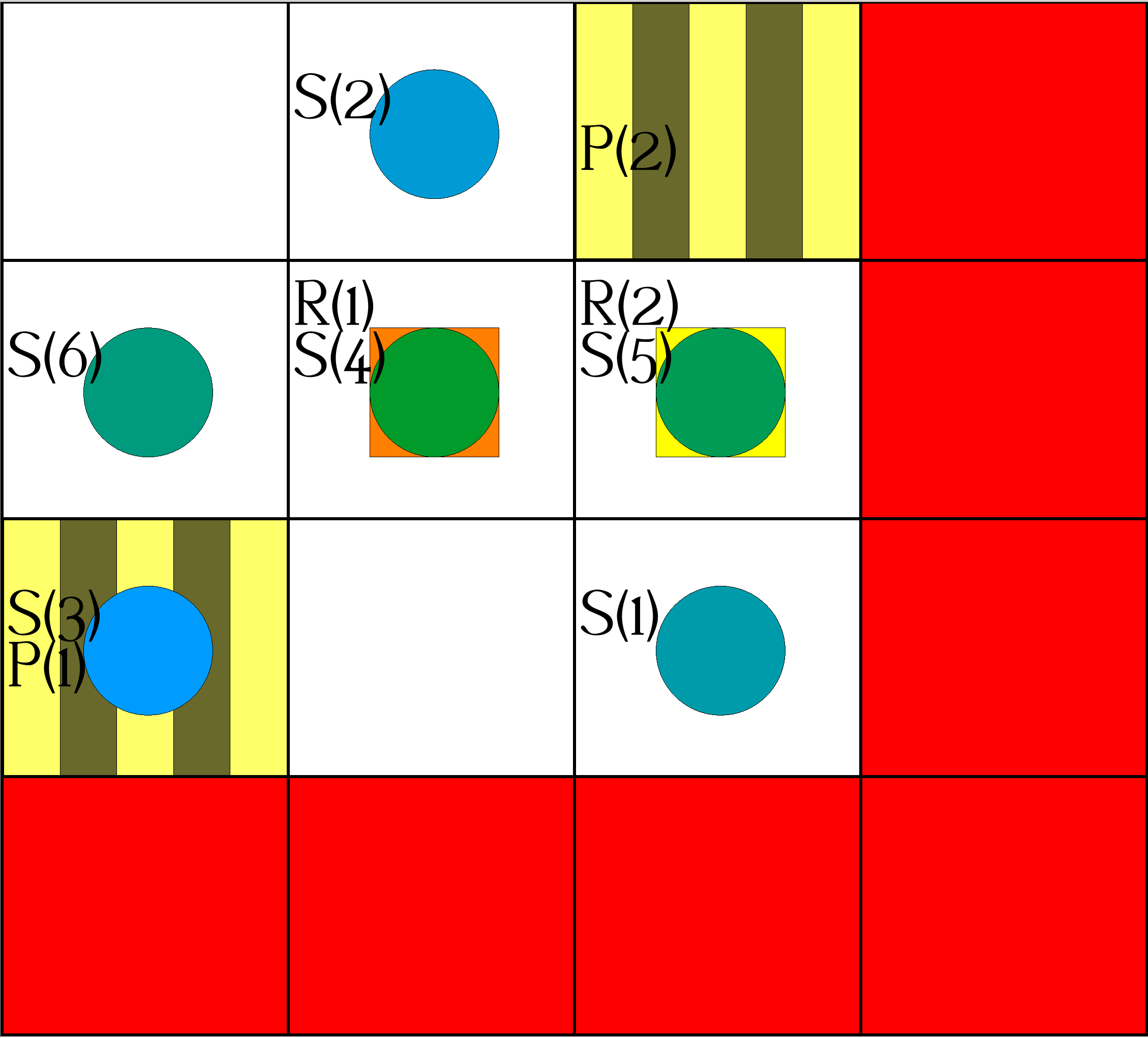 |
occurs(object(robot,1),move(0,-1),9). occurs(object(robot,2),pickup,9). |
| Step 10: | Actions: |
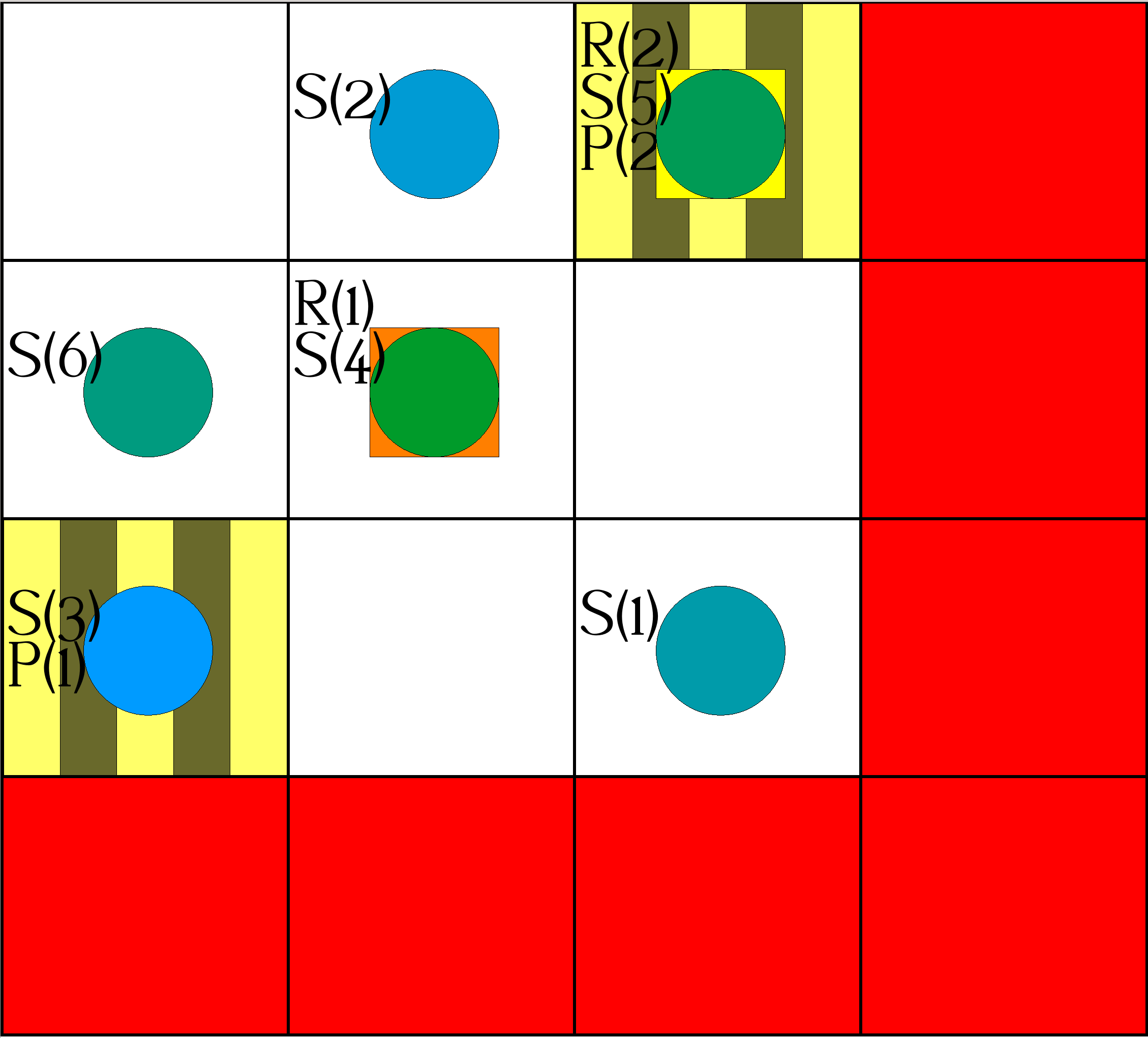 |
occurs(object(robot,1),pickup,10). occurs(object(robot,2),move(0,-1),10). |
| Step 11: | Actions: |
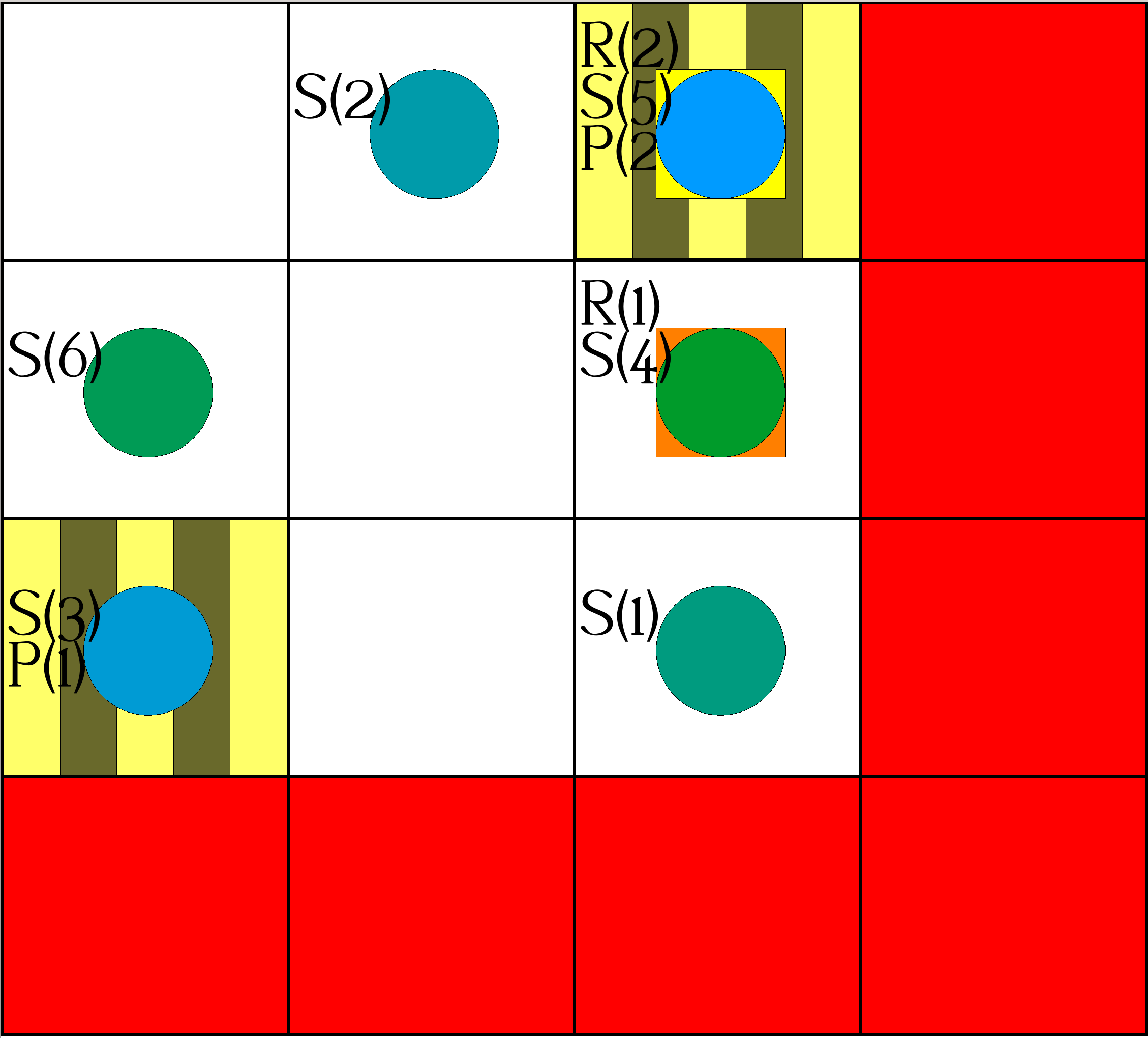 |
occurs(object(robot,1),move(1,0),11). occurs(object(robot,2),deliver(3,4,1),11). |
| Step 12/13: | Actions: |
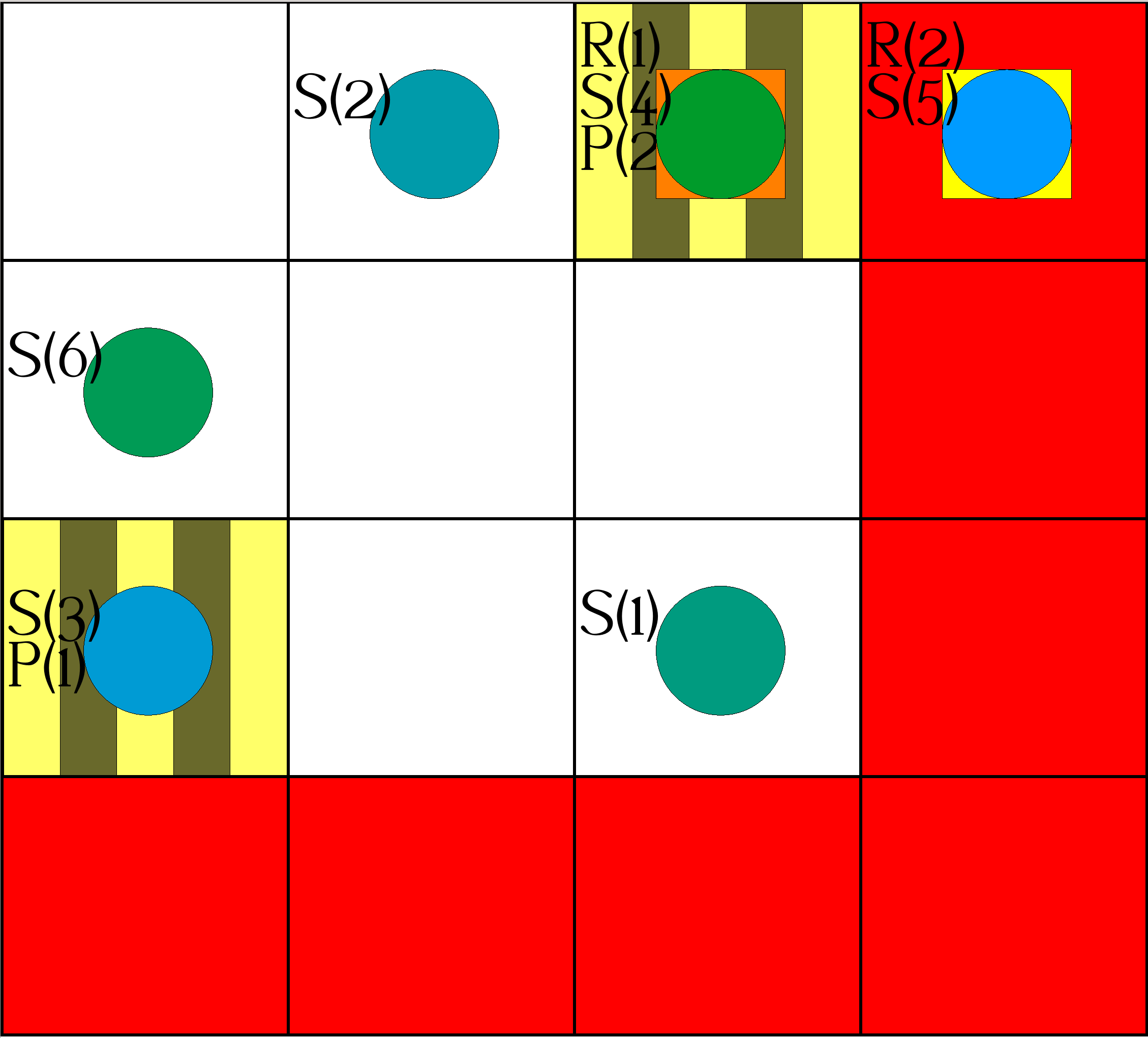 |
occurs(object(robot,1),move(0,-1),12). occurs(object(robot,2),move(1,0),12). occurs(object(robot,1),deliver(2,2,1),13). |
System Submission
Systems in the ASP Model&Solve Competition have to comply with the input/output interface used since the ASP Competition 2017. (Note that a system input contains only facts specifying an automated warehouse scenario, while a full-fledged ASP-Core-2 encoding would also admit rules, weak constraints and queries.) Systems will be executed on a single processor core, imposing a wall time limit of 1 hour and a memory limit of 6 GB. (Imminent runtime exhaustion will be signaled to a system by the competition environment to allow for outputting the best solution found so far in the time still remaining; respective details about the competition environment will be sent after system registration.) A number of example instances as well as a solution checker are available for download. For registering a team, which may submit one or more systems, to the ASP Model&Solve Competition, please send a brief statement of interest by mail to the organizers (Martin Gebser, Marco Maratea and Francesco Ricca) via Questo indirizzo email è protetto dagli spambots. È necessario abilitare JavaScript per vederlo. by June 18, 2017. Access to the competition platform, in order to install and test systems, will then be provided from 12:00 CET on June 19, 2017 to 12:00 CET on June 22, 2017 (tentative).

